How To Find Under Root Of Any Number

Get this volume -> Problems on Array: For Interviews and Competitive Programming

Reading time: 35 minutes | Coding fourth dimension: 10 minutes

Equally the title sugests, Root-Finding Problem is the problem of finding a root of an equation f(x) = 0, where f(ten) is a function of a single variable 10. The trouble is stated as follows:

Given a continuous function f(x).
Find a number x = c such that f(c) = 0.

The number x = c such that f(c) = 0 is called a root of the equation f(x) = 0 or a goose egg of the function f(x).

The root-finding problem is one of the about important computational issues. It arises in a wide variety of practical applications in physics, chemistry, biosciences, engineering science, etc.

Why use Numerical Methods for Root Finding Problems ?

Except for some very special functions, it is not possible to find an analytical expression for the root, from where the solution tin be exactly determined.

You may have learned how to solve a quadratic equation :
fig

Unfortunately, such belittling formulas exercise non exist for polynomials of degree 5 or greater as stated by Abel–Ruffini theorem.

Thus, about computational methods for the root-finding problem take to be iterative in nature. The main idea is to offset take an initial approximation of the root and produce a sequence of numbers (each iteration providing more accurate approximation to the root in an platonic case) that volition converge towards the root. Since the iteration must be stopped at some bespeak these methods produce an approximation to the root, not an exact solution.

In this post we wil explore:

Bisection Method

Bisection Method

Theory

The Bisection Method, also chosen the interval halving method, the binary search method, or the dichotomy method is based on the Bolzano's theorem for continuous functions (corollary of Intermediate value theorem).

Theorem (Bolzano) : If the function f(x) is continuous in [a, b] and f(a)f(b) < 0 (i.e. f(ten) has opposite signs signs at a and b)
then a value c ∈ (a, b) exists such that f(c) = 0.

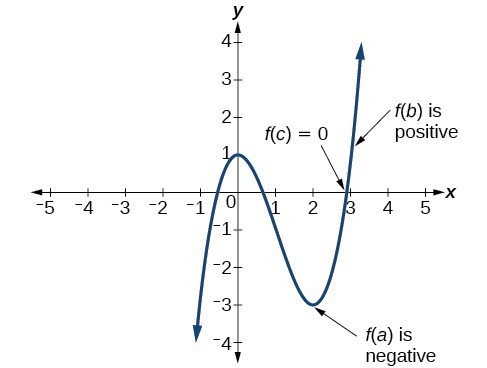
fig1.1

The Bisection Method looks to discover the value c for which the plot of the function f crosses the x-axis. The c value is in this case is an approximation of the root of the part f(x). How close the value of c gets to the existent root depends on the value of the tolerance we set for the algorithm.

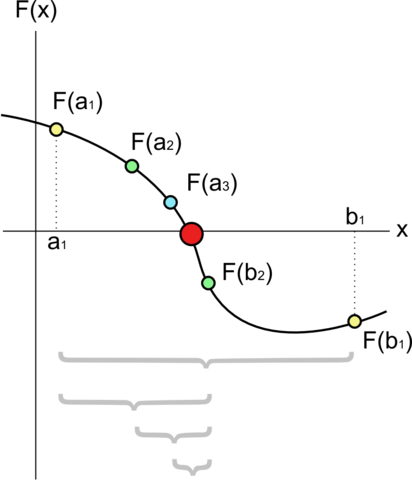
Prototype: Bisection Method practical to a function F(x) with initial guesses every bit a1 and b1.
Image Source : https://en.wikipedia.org/wiki/File:Bisection_method.png

Algorithm

For a given office f(x),the Bisection Method algorithm works every bit follows:

              one. Start  2. Ascertain part f(x)  3. Input  	a. Lower and Upper guesses a and b 	b. tolerable error e 	 4. If f(a)*f(b) > 0 	print "Wrong initial guesses"    	goto 3    End If  5. Do  	c = (a+b)/2 	 	If f(a)*f(c) < 0 		b = c 	Else 		a = c 	End If 		    while (fabs(f(c)) > east)   // fabs -> returns absolute value      6. Print root every bit c  7. Stop

Sample Trouble

Now allow's work with an example:

Show that f(ten) = x³ + 4x^two - 10 has a root in [1,ii], and utilise the Bisection method to determine an approximation to the root that is accurate to at least within x^-vi.

At present, the information required to perform the Bisection Method is as follow:

f(x) = tenⁱⁱⁱ + 4x² - 10,
Lower Estimate a = one,
Upper Guess b = 2,
And tolerance eastward = 10^-6

We know that f(a) = f(1) = -5 (negative) andf(b) = f(2) = 14 (positive) and so the Intermediate Value Theorem ensures that the root of the function f(x) lies in the interval [one,2].

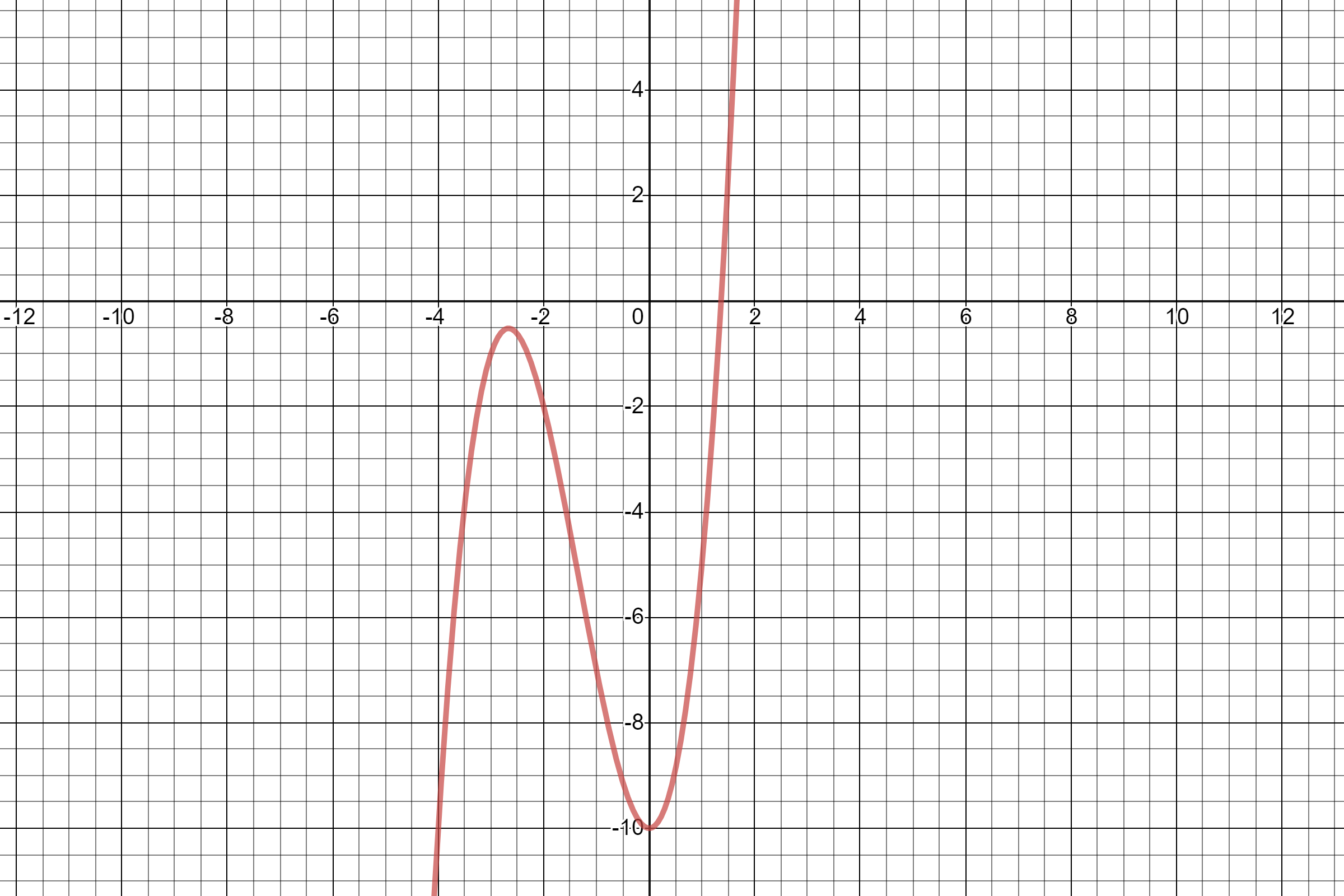
Figure: Plot of the function f(x) = 10³ + 4x² - x

Beneath we show the iterative process described in the algortihm in a higher place and show the values in each iteration:

Inputs
- f(10) = x³ + 4x² - 10,
- Lower Guess a = 1,
- Upper Gauge b = two,
- And tolerance e = 10^-6

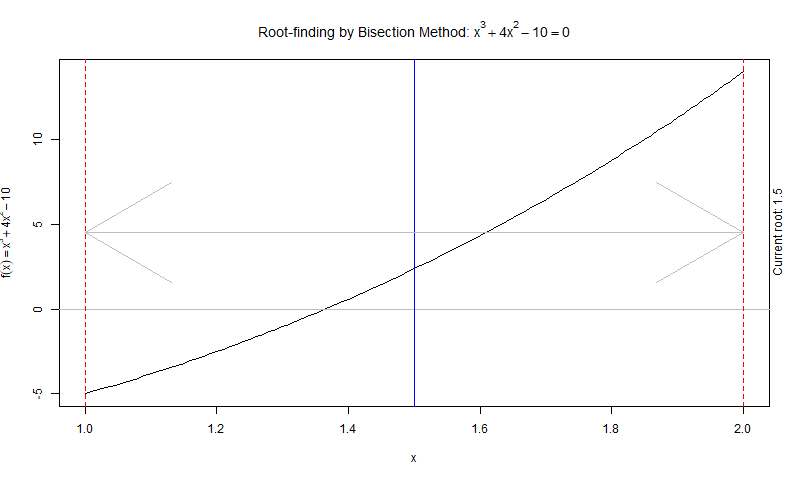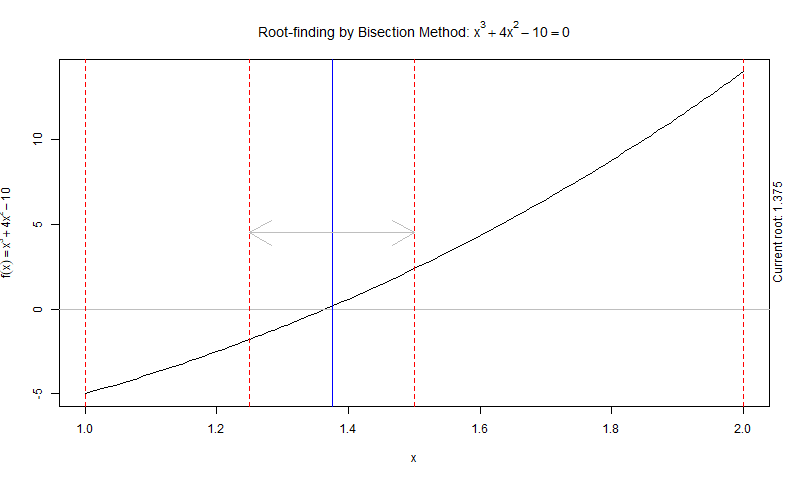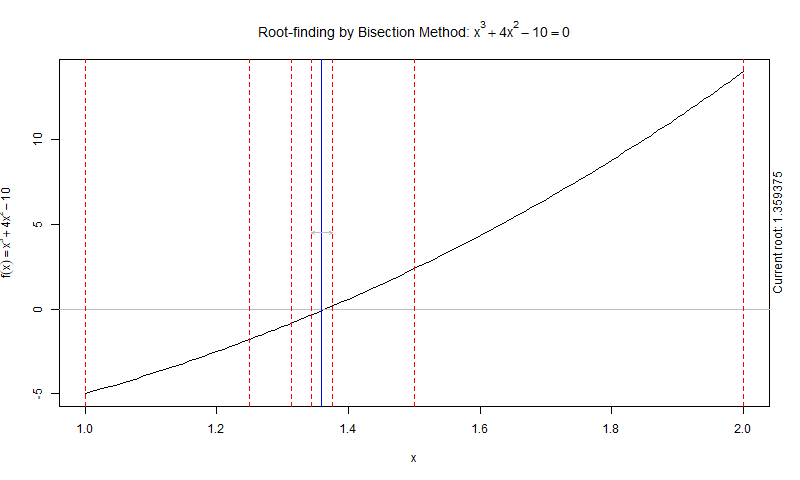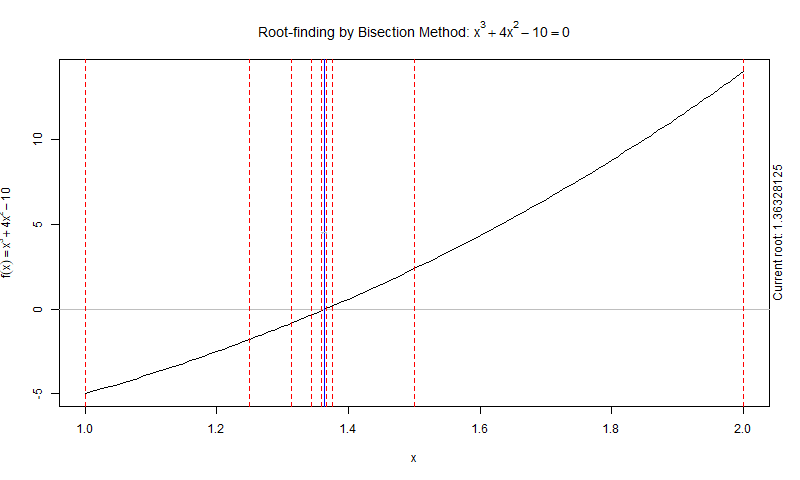
Iteration 1
a = 1, b = 2

Bank check if f(a) and f(b) have opposite signs
f(a) = f(1) = -v ; f(b) = f(2) = 14
Then, f(a)*f(b) = f(i)*f(2) = -lxx < 0 ✅
We so proceed to calculate c :
c = (a+b)/two = (1+2)/2 = 1.5
c=one.5
Cheque if f(a) and f(c) have opposite signs
f(a) = f(ane) = -five ; f(c) = f(1.5) = ii.375
f(a)*f(c) = f(1)*f(i.5) = -11.875 < 0 ✅
Since the above status is satisfied, we make c as our new upper approximate i.e. b
b = c
b = 1.5
So, we have reduced the interval to half of the original.
[1,ii] -> [1,1.v]
Now we cheque the loop condition i.e. fabs(f(c)) > e
f(c) = two.375
fabs(f(c)) = 2.375 > e = 10^-vi ✅
The loop condition is true so we will perform the adjacent iteration.

Iteration 2
a = 1, b = 1.5

Cheque if f(a) and f(b) have opposite signs
f(a) = f(ane) = -five ; f(b) = f(one.5) = 2.375
Then, f(a)*f(b) = f(1)*f(1.5) = -11.875 < 0 ✅
Nosotros so proceed to calculate c :
c = (a+b)/two = (1+1.5)/2 = 1.25
c=1.25
Check if f(a) and f(c) take opposite signs
f(a) = f(1) = -5 ; f(c) = f(ane.25) = -i.796875
f(a)*f(c) = f(i)*f(i.25) = viii.984375 < 0 ❌
Since the above condition is non satisfied, we make c equally our new lower approximate i.due east. a
a = c
a = one.25
Again we take reduced the interval to half of the original.
[one,i.5] -> [1.25,1.5]
Now we check the loop condition i.e. fabs(f(c)) > e
f(c) = -1.796875
fabs(f(c)) = i.79685 > e = 10^-6 ✅
The loop status is truthful so we volition perform the side by side iteration.

As you lot can see, the Bisection Method converges to a solution which depends on the tolerance and number of iteration the algorithm performs.

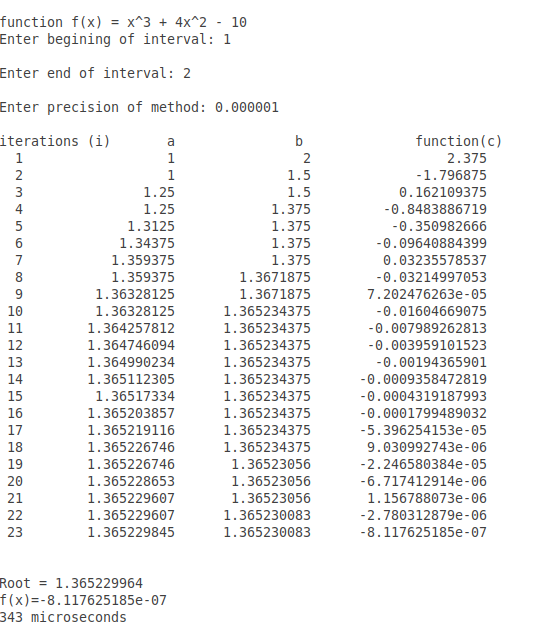
Bisection Method Iterations for the function f(x) = 10^three + 4x² - ten

bisection_method3

C++ Implementation

              #include <iostream> #include <math.h> #include<iomanip> #include<chrono> using namespace std::chrono;  using namespace std;   static double function(double x); // role f(ten) void carte du jour();   int master() {      double a; // Lower Guess or commencement of interval   double b; // Upper Guess or end of interval   double c; // variable for midpoint   double precision;     cout << "\north\n\nfunction f(x) = 10^three + 4x^2 - 10  "<<endl;      // Taking Input   cout << "Enter begining of interval: ";   cin >> a;   cout << "\nEnter end of interval: ";   cin >> b;   cout << "\nEnter precision of method: ";   cin >> precision;    // Check for contrary sign (Intermediate Value Theorem)   if (function(a) * function(b) > 0.0f)   {     cout << "\nFunction has same signs at ends of interval";     return -ane;   }  int iter=0; cout<<setw(3)<<"\niterations (i)"<<setw(8)<<"a"<<setw(16)<<"b"<<setw(25)<<"function(c)"<<endl;  auto start = high_resolution_clock::at present();     practice   {     c = (a + b) / 2.0f;      iter++;     cout<<setprecision(10)<<setw(3)<<iter<<setw(nineteen)<<a<<setw(17)<<b<<setw(22)<<function(c)<<endl;      // check for contrary sign     if (function(a) * function(c) < 0.0f)     {       b = c;     }     else     {       a = c;     }   }while (fabs(function(c))>=precision);  // terminating condition    auto finish = high_resolution_clock::now();    motorcar duration = duration_cast<microseconds>(stop - outset);     cout<<"\due north\nRoot = "<<c<<endl;   cout<<"f(10)="<<office(c)<<endl;   cout << duration.count()<<" microseconds"<< endl;     return 0; }  static double part(double 10) {   return pow(x,3) + 4*pow(x,2) - x ; }

Another Example

Bisection Method Iterations for the function f(x) = log(10) - cos(10) with a = 1, b = 1.5 and tolerance = ten^-9

Limitations

While Bisection Method is e'er convergent, significant that it is always leading towards a definite limit and relatively elementary to understand there are some drawbacks when this algorithm is used.

Tedious rate of convergence
The convergence of the bisection method is irksome as it is simply based on halving the interval.
Relies on sign changes
If a function f (10) is such that it but touches the x -centrality for example say f(x) = 10^two and so it volition not be able to discover lower guess (a) such that f(a)*f(b) < 0
Cannot notice Multiple Roots
The Bisection method fails to place multiple different roots, which makes information technology less desirable to apply compared to other methods that tin identify multiple roots. When an equation has multiple roots, it is the choice of the initial interval provided by the user which determines which root is located.

Question

After one iteration of the Bisection Method, by how much did our interval that might contain a zippo of the function decrease?

More than 50%

Less than fifty%

At each stride the method divides the interval in 2 by computing the midpoint c = (a+b) / 2 of the interval. The method selects the subinterval that is guaranteed to be a subclass as the new interval (by checking the opposite signs) to be used in the adjacent pace. In this fashion an interval that contains a zero of the function is reduced in width by l% at each step.