How To Find Regression Equation By Hand

Principles of Linear Regression

Linear regression is a method for predicting y from ten. In our example, y is the dependent variable, and x is the independent variable. We desire to predict the value of y for a given value of ten. At present, if the data were perfectly linear, we could simply calculate the gradient intercept form of the line in terms y = mx+ b . To predict y , we would just plug in the given values of x and b. In the real world, our information will non be perfectly linear. It will likely be in the form of a cluster of data points on a scatterplot. From that scatterplot, we would like to make up one's mind, what is the line of best fit that describes the linear qualities of the information, and how well does the line fit the cluster of points?

Linear regression attempts to model the human relationship between two variables past fitting a linear equation to observed data (Linear Regression, n.d.).

Scatterplots

Let's make up some data to use as an example. The relationship between Chimpanzee hunting party size and percentage of successful hunts is well documented. (Busse, 1978) I am going to catch a few information points from Busse to utilise for this article, and plot the data using a seaborn scatterplot. Observe how the line I drew through the data does not fit information technology perfectly, but the points judge a linear pattern? The line I drew through the data is the Least Squares Line, and is used to predict y values for given x values . Using just a rudimentary Least Squares Line drawn by paw through the information, we could predict that a hunting party of 4 chimpanzees is going to be around 52% successful. We are not 100 percent accurate, but with more information, we would likely amend our accuracy. How well the data fits the Least Squares Line is the Correlation Coefficient.

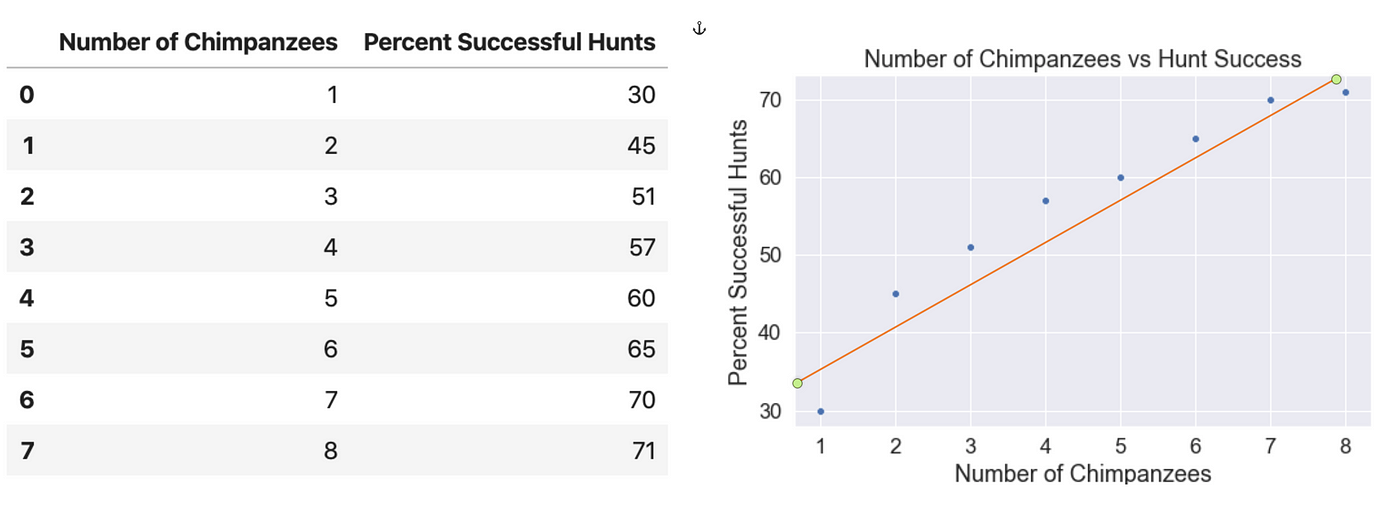
Least Squares Line

In the chart above, I merely drew a line by paw through the data that I judged to exist the best fit. We should calculate this line in slope intercept form y = mx + b to make truthful predictions. What we are seeking is a line where the differences betwixt the line and each indicate are as modest as possible. This is the line of all-time fit.

The least squares line is divers as the line where the sum of the squares of the vertical distances from the data points to the line is equally minor every bit possible (Lial, Greenwell and Ritchey, 2016).

The least squares line has two components: the slope grand, and y-intercept b. We volition solve for m first, and then solve for b. The equations for one thousand and b are:

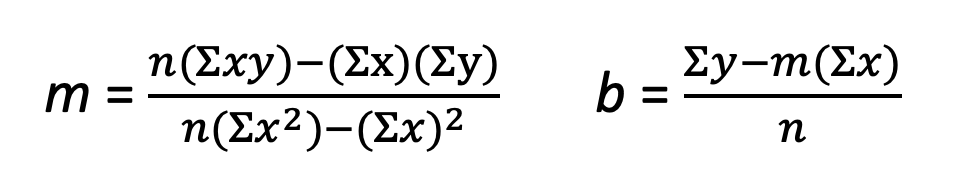
That's a lot of Sigmas (∑)!. But don't worry, Sigma merely means "sum of", such every bit "sum of x," symbolized by ∑x, which is but the sum of the x column, "Number of Chimpanzees." Nosotros need to calculate ∑x, ∑y, ∑xy, ∑x², and ∑y². Each piece will then be fed into the equations for thou and b. Create the beneath table based on our original dataset.

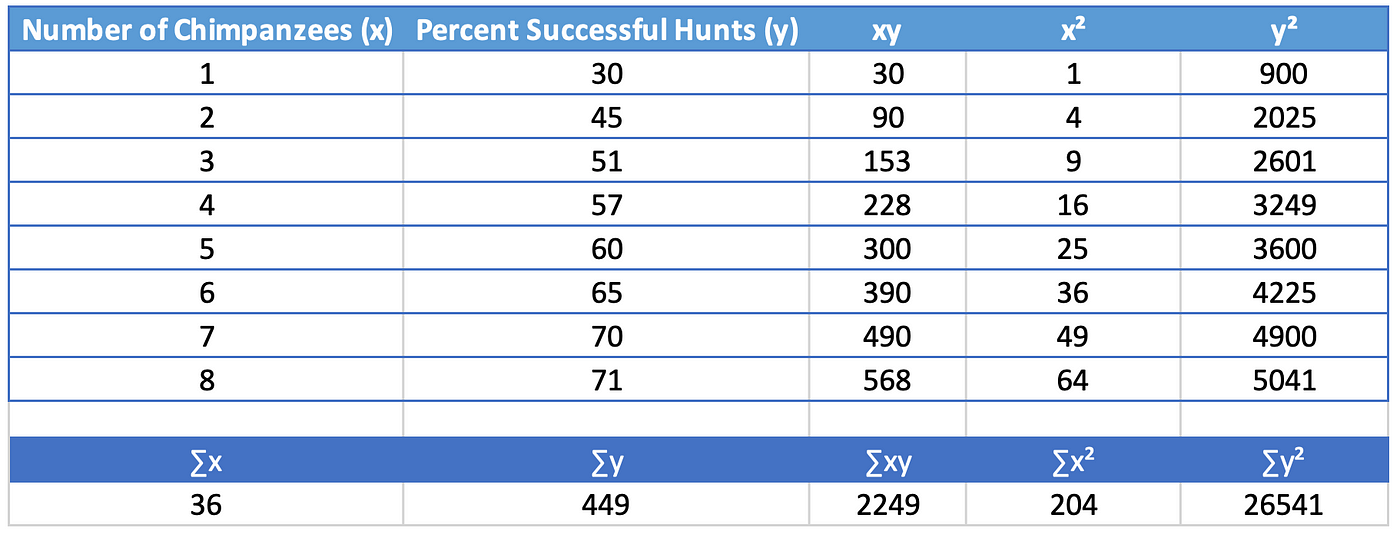
At present it is a simple affair to plug our Sigma values into the equation for 1000 and b. n is the number of values in the dataset, which in our example is 8.

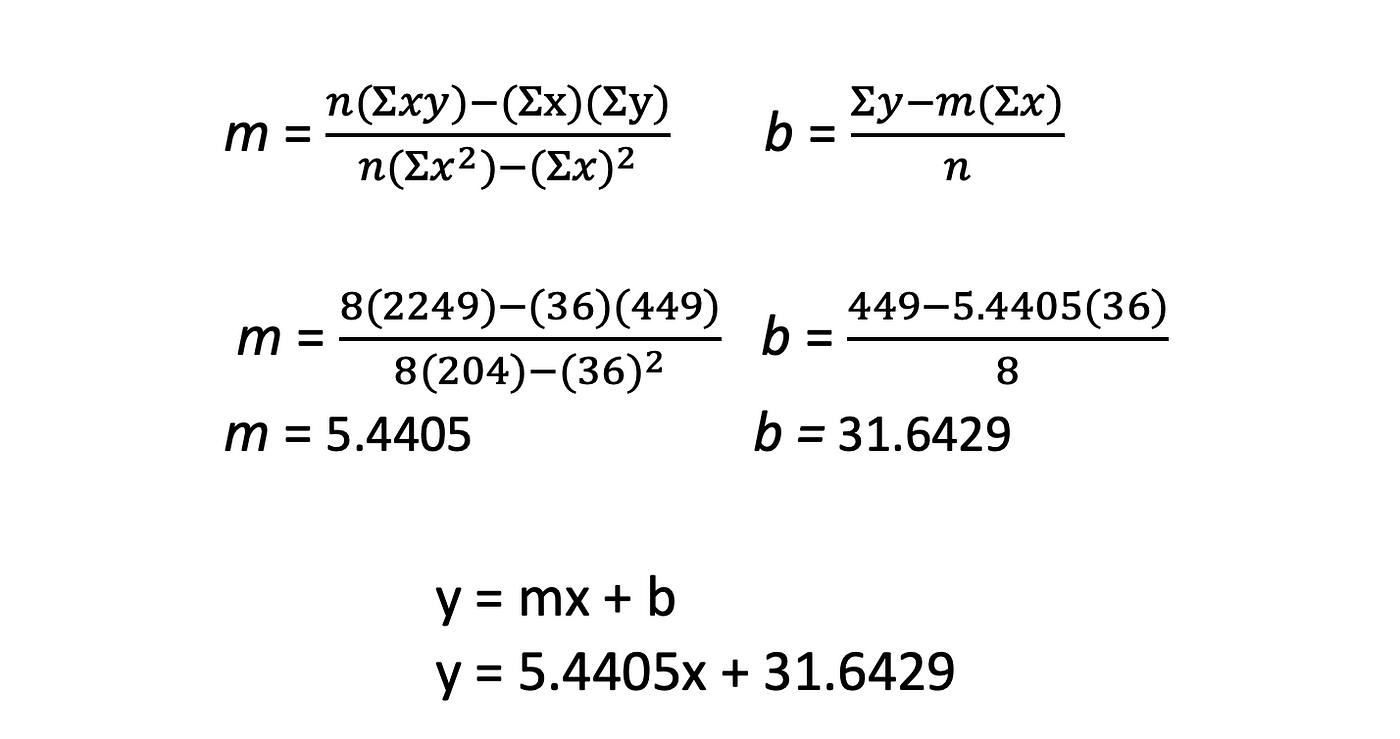
There you take it! Yous can make predictions of y from given values of x using your equation: y = five.4405x + 31.6429. This means that our line starts out at 31.6429 and the y-values increase by 5.4405 percentage points for every 1 Chimpanzee that joins the hunting party. To exam this out, let's predict the percent hunt success for iv chimpanzees.

                                    y = v.4405(4)+31.6429            , which results in            y=53.four

We just predicted the percentage of successful hunts for a chimpanzee hunting political party based solely on cognition of their group size, which is pretty amazing!

Permit'southward plot the least squares line over our previous scatterplot using python to testify how it fits the data. Seaborn.regplot() is a great nautical chart to apply in this situation, only for demonstration purposes, I will manually create the y=mx+b line and lay it over the seaborn chart.

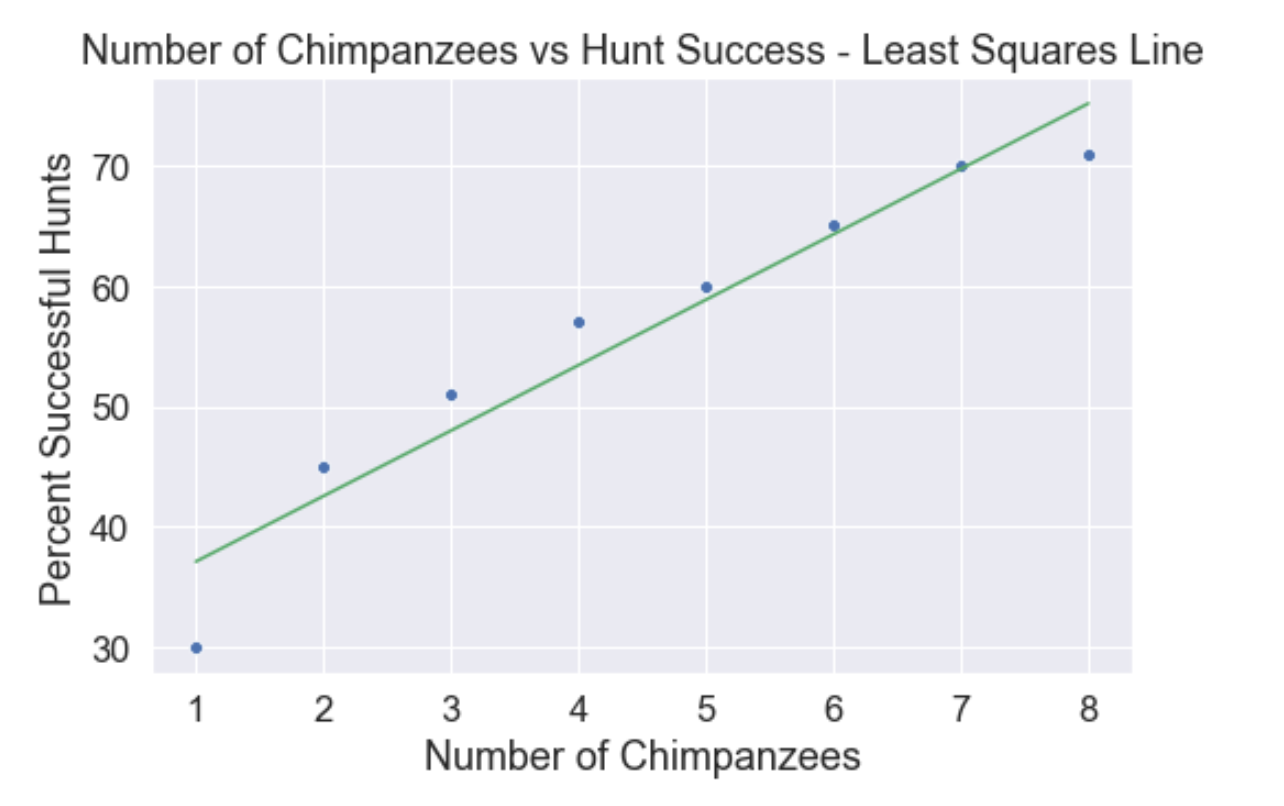
Yet, now that you tin can brand predictions, you demand to qualify your predictions with the Correlation Coefficient, which describes how well the data fits your calculated line.

Correlation Coefficient

We use the Correlation Coefficient to determine if the least squares line is a good model for our data. If the data points are not linear, a straight line will not be the correct model for prediction. Karl Pearson invented the Correlation Coefficient r , which is betwixt 1 and -1, and measures the strength of the linear relationship between two variables (Lial, Greenwell and Ritchey, 2016). If r is exactly -1 or 1, it ways the data fits the line exactly, and there is no difference from the line. r=0 means that there is no linear correlation. As r values approach nix, it means that association decreases as well.

The Correlation Coefficient is described by the formula

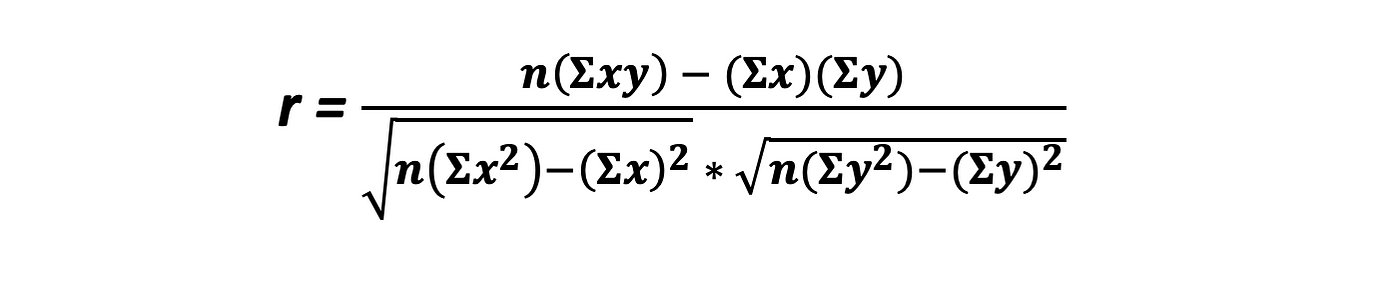
Luckily, these Sigma values take already been calculated in our previous table. We simply plug them into our equation.

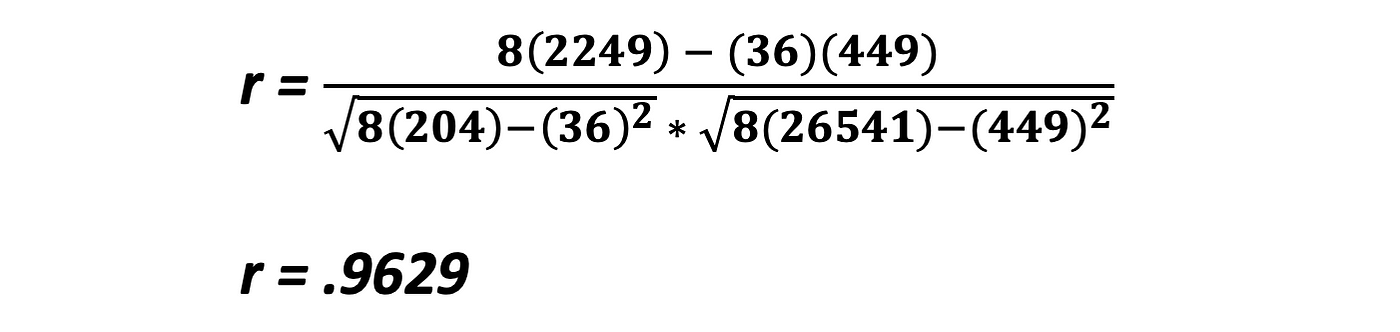
Our value is close to positive 1, which ways that the information is highly correlated, and positive. Yous could have determined this from looking at the least squares line plotted over the scatterplot, simply the Correlation Coefficient gives you lot scientific proof!

Conclusion

Linear regression is one of the best motorcar learning methods available to a data scientist or a statistician. There are many ways to create a machine learning model using your programming skills, only it is definitely a practiced idea to familiarize yourself with the math used by the model.